Linvis Blog

Redis基本数据结构-1

2020-06-07

string

这里关注几个重点API，创建、扩容、释放

数据结构

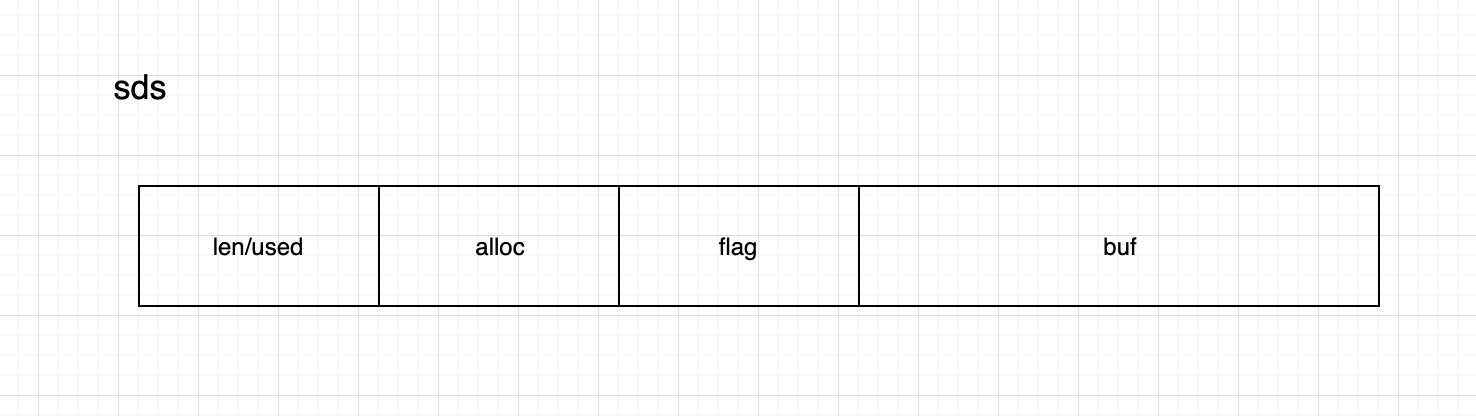
image-20200531165943541

sds是string存储的基本单元

在C语言中，string是以\0结尾，对于本身就包含\0的string来说，会被C语言意外截断，为了解决这个问题，redis采用了保存string长度的方法

redis按照string的长度，划分了5类数据，分别表征$2^5, 2^8, 2^16, 2^32, 2^{64}$的长度

1
2
3
4
5
#define SDS_TYPE_5  0
#define SDS_TYPE_8  1
#define SDS_TYPE_16 2
#define SDS_TYPE_32 3
#define SDS_TYPE_64 4

第二，每种sds，有三个头部信息(SDS_TYPE_5有两个)，分别是总长度，已使用的长度，字符串类型

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
/* Note: sdshdr5 is never used, we just access the flags byte directly.
 * However is here to document the layout of type 5 SDS strings. */
struct __attribute__ ((__packed__)) sdshdr5 {
    unsigned char flags; /* 3 lsb of type, and 5 msb of string length */
    char buf[];
};
struct __attribute__ ((__packed__)) sdshdr8 {
    uint8_t len; /* used */
    uint8_t alloc; /* excluding the header and null terminator */
    unsigned char flags; /* 3 lsb of type, 5 unused bits */
    char buf[];
};
struct __attribute__ ((__packed__)) sdshdr16 {
    uint16_t len; /* used */
    uint16_t alloc; /* excluding the header and null terminator */
    unsigned char flags; /* 3 lsb of type, 5 unused bits */
    char buf[];
};
struct __attribute__ ((__packed__)) sdshdr32 {
    uint32_t len; /* used */
    uint32_t alloc; /* excluding the header and null terminator */
    unsigned char flags; /* 3 lsb of type, 5 unused bits */
    char buf[];
};
struct __attribute__ ((__packed__)) sdshdr64 {
    uint64_t len; /* used */
    uint64_t alloc; /* excluding the header and null terminator */
    unsigned char flags; /* 3 lsb of type, 5 unused bits */
    char buf[];
};

每个结构体都是packed的，可以很方便的根据buf，获取到len、alloc、flags等字段

buf地址返回给上层api，完美的兼容C

sdsnewlen

1
sds sdsnewlen(const void *init, size_t initlen)

  • 根据initlen，设置成不同的type

  • 创建并初始化sdshdr结构体

  • malloc和memcpy字符串

这里，len和alloc都被初始化成initlen，即new的时候，不存在free的数据

sdscatlen

1
sds sdscatlen(sds s, const void *t, size_t len)

本质即扩容

  • 判断free len是否满足
  • 不满足则扩容，新长度小于1M，直接2倍扩容，大于1M，+1M扩容
  • 判断扩容后type是否变化，无变化realloc申请，否则malloc
  • 扩容完，拷贝拼接，更新sdshdr结构体

sdsfree

1
void sdsfree(sds s)

很简单，通过s找到sdshdr结构体的指针，代用zfree释放

总结

  • sds的数据结构

  • packed，结构体寻址

  • 如何扩容

    < 1M，2倍扩容，> 1M， + 1M

跳跃表(zskiplist)

跳跃表是一种用空间换时间的算法，比红黑树实现简单，效率差不多，其查找的时间复杂度是$O(\log{N})$

核心思想

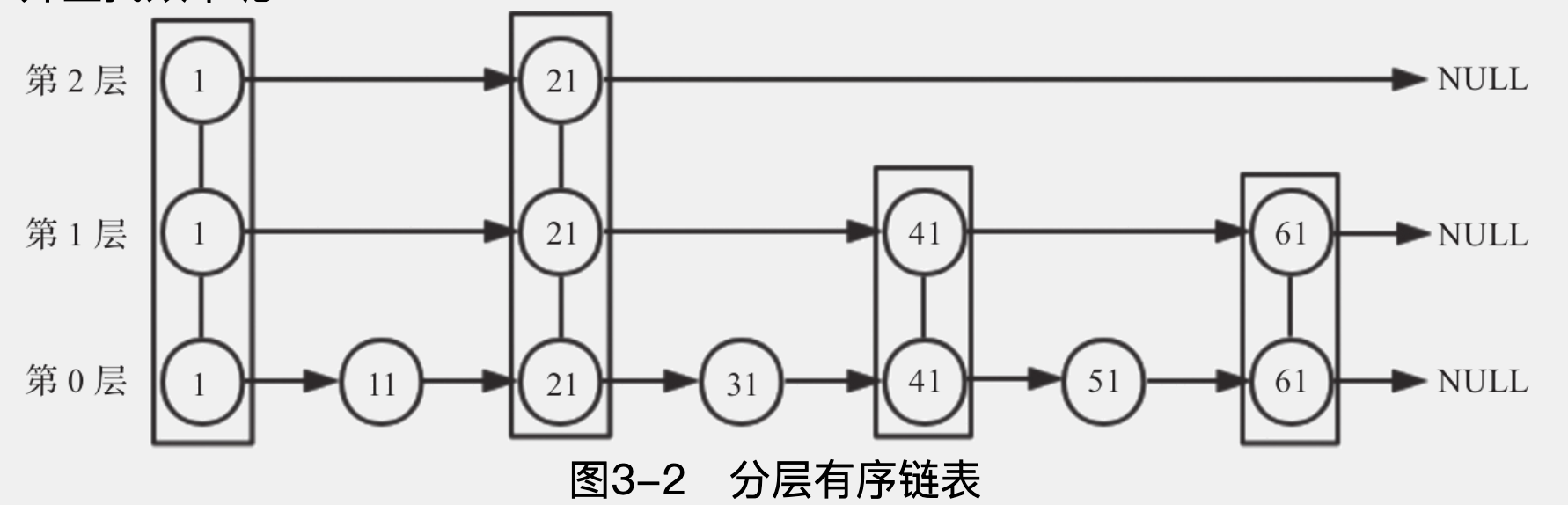
image-20200531170652818

跳跃表通过分层，减少遍历的范围

跳跃表本质上，是一种二分的思想，由于链表在查找上是$O(N)$的时间复杂度，为了降低这个复杂度，通过构建额外的有序链表(存储”二分节点”)，来加快遍历

数据结构

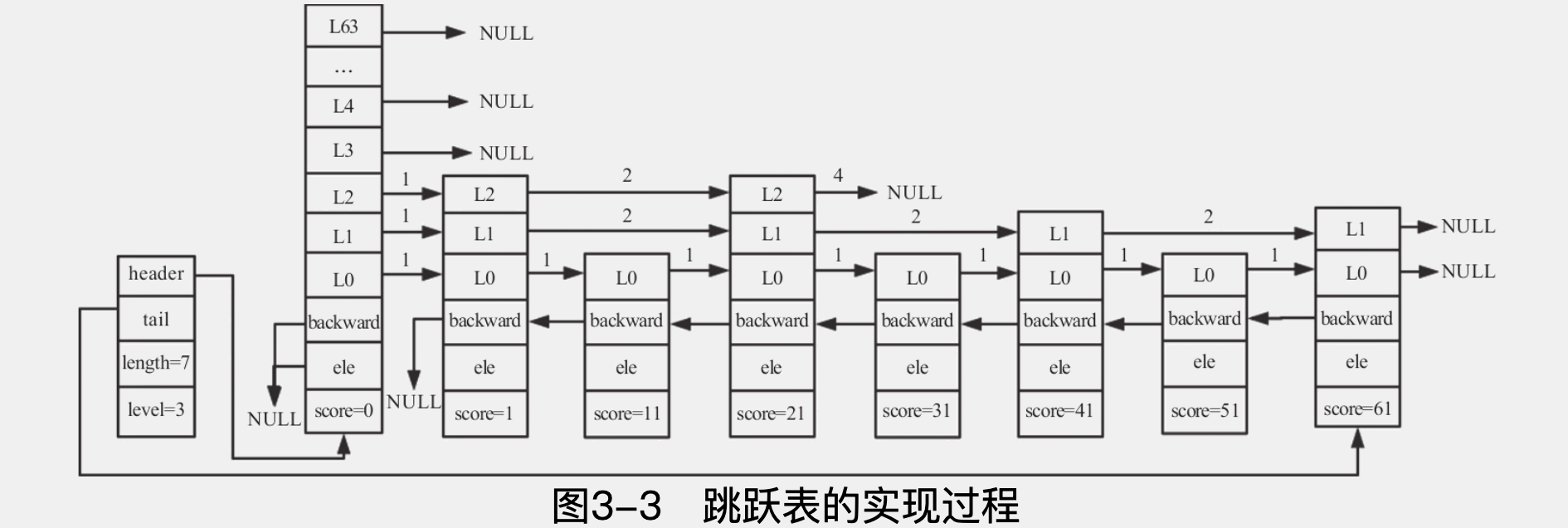
image-20200531171624624

6.0.3里L的高度变成了32，而不是64

上图容易造成一个错觉，L0可能指向下一个L0的地址，实际上，L0的forward指针，指向的是下一个zskiplistNode

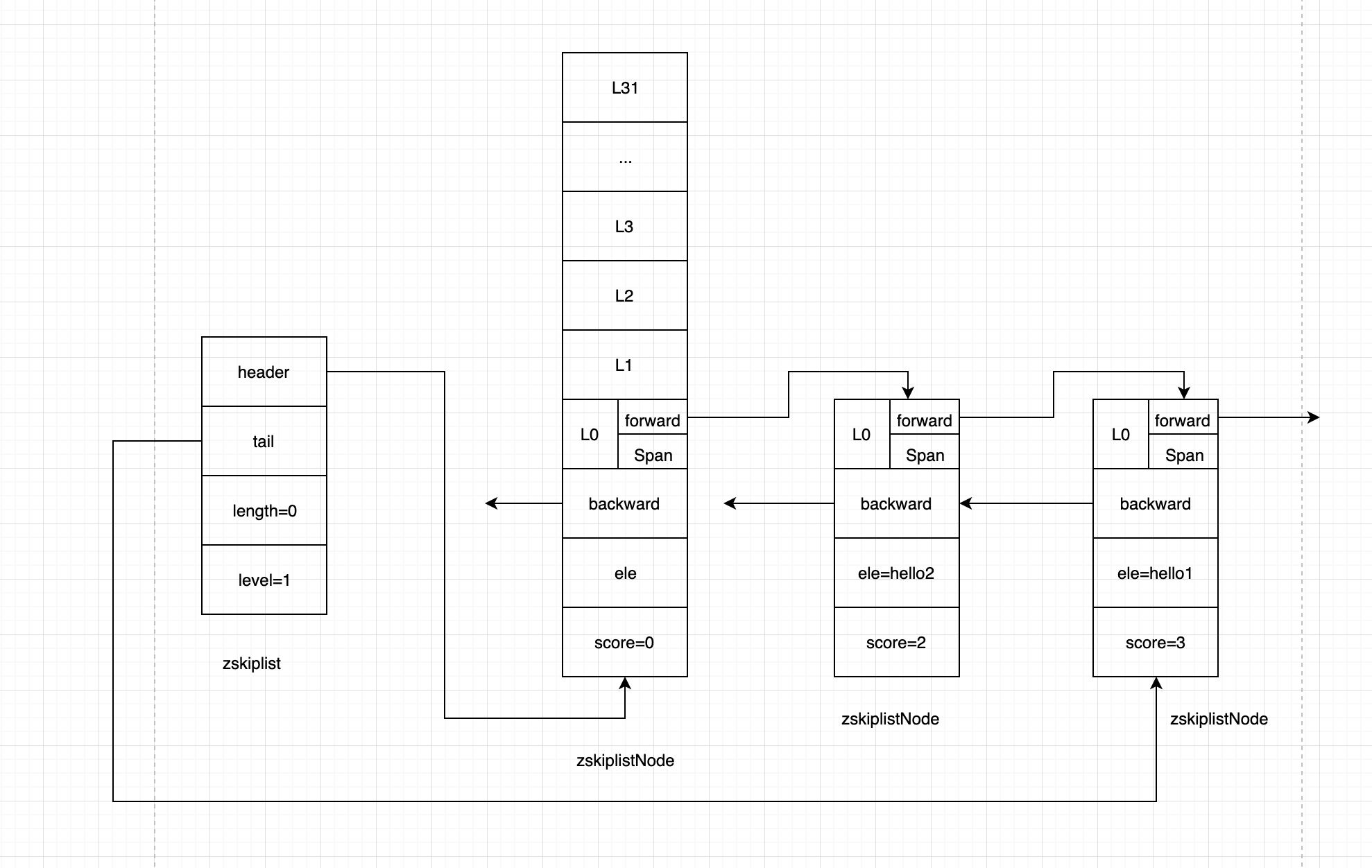
image-20200531173139177

这里有几个重要的数据

  • zskiplist的level

    1
    level = max(all len(zskiplistNode.level[]))

  • zskiplist的length

    所有zskiplistNode的个数

  • zskiplistNode的span

    步长的意思，表示和上一个zskiplistNode，中间隔了多少个L0层的node节点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
typedef struct zskiplist {
    struct zskiplistNode *header, *tail;
    unsigned long length;
    int level;
} zskiplist;

// forward指向下一个节点
// backward指向前一个节点
typedef struct zskiplistNode {
    sds ele;
    double score;
    struct zskiplistNode *backward;
    struct zskiplistLevel {
        struct zskiplistNode *forward;
        unsigned long span;
    } level[];
} zskiplistNode;

创建

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#define ZSKIPLIST_MAXLEVEL 32 /* Should be enough for 2^64 elements */

/* Create a new skiplist. */
zskiplist *zslCreate(void) {
    int j;
    zskiplist *zsl;

    zsl = zmalloc(sizeof(*zsl));
    zsl->level = 1;
    zsl->length = 0;
    zsl->header = zslCreateNode(ZSKIPLIST_MAXLEVEL,0,NULL);
    for (j = 0; j < ZSKIPLIST_MAXLEVEL; j++) {
        zsl->header->level[j].forward = NULL;
        zsl->header->level[j].span = 0;
    }
    zsl->header->backward = NULL;
    zsl->tail = NULL;
    return zsl;
}

这个函数比较简单，初始化zskiplist结构体，创建header节点

插入

  1. 查找要插入的位置
  2. 调整跳跃表的高度
  3. 插入节点
  4. 调整backward

查找

整个查找过程如下图的路径，当发现score <= next node’s score，即转向下一层

image-20200531174142478

1
2
3
4
5
6
7
8
9
10
11
12
13
14
x = zsl->header;
for (i = zsl->level-1; i >= 0; i--) {
    /* store rank that is crossed to reach the insert position */
    rank[i] = i == (zsl->level-1) ? 0 : rank[i+1];
    while (x->level[i].forward &&
            (x->level[i].forward->score < score ||
                (x->level[i].forward->score == score &&
                sdscmp(x->level[i].forward->ele,ele) < 0)))
    {
        rank[i] += x->level[i].span;
        x = x->level[i].forward;
    }
    update[i] = x;
}

这里使用了两个临时数组update, rank

每次发生level—，即意味着，已经找到了新节点要插入的位置，这时候，把位置节点缓存到update上，把位置节点的span缓存到rank上

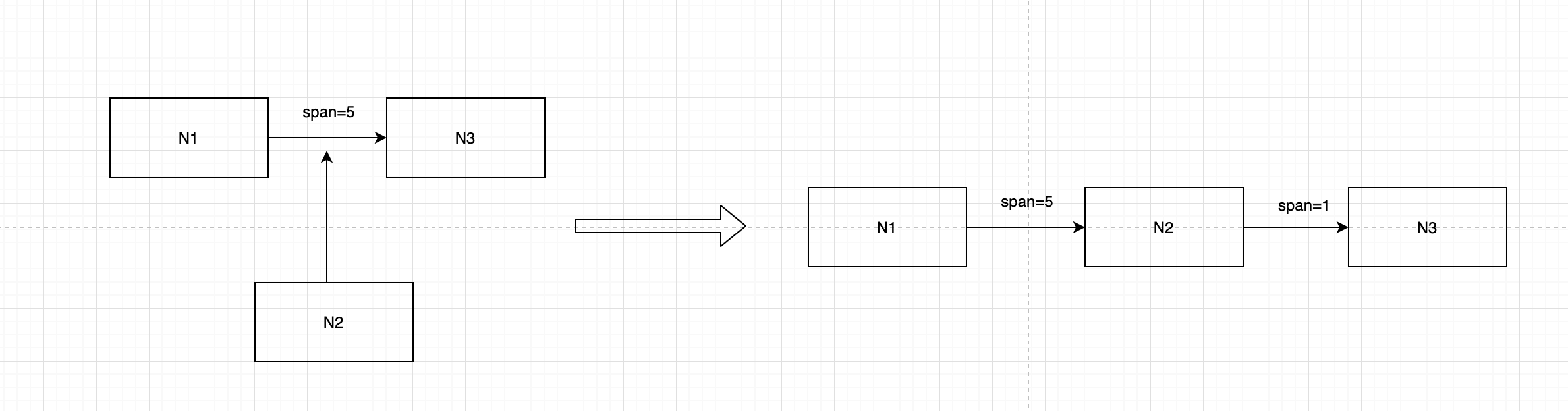
image-20200531175300049

N2占据的N3的位置，N2和N3由于之间没有节点了，所以span=1

创建新节点

创建新节点会随机一个level出来，如果比当前的level大，那么更新zskiplist的level

所以redis更新level是随机的，$level=p^{n-1}(1-p), p = ZSKIPLIST_P=0.25$

level的数学期望是1.33

1
2
3
4
5
6
7
8
9
10
level = zslRandomLevel();
if (level > zsl->level) {
    for (i = zsl->level; i < level; i++) {
        rank[i] = 0;
        update[i] = zsl->header;
        update[i]->level[i].span = zsl->length;
    }
    zsl->level = level;
}
x = zslCreateNode(level,score,ele);

更新节点

把新节点x，插入到各个level中，并且更新span

1
2
3
4
5
6
7
8
9
10
11
12
13
  // x = zslCreateNode(level,score,ele)
for (i = 0; i < level; i++) {
      x->level[i].forward = update[i]->level[i].forward;
      update[i]->level[i].forward = x;

      /* update span covered by update[i] as x is inserted here */
      x->level[i].span = update[i]->level[i].span - (rank[0] - rank[i]);
      update[i]->level[i].span = (rank[0] - rank[i]) + 1;
  }
  /* increment span for untouched levels */
  for (i = level; i < zsl->level; i++) {
      update[i]->level[i].span++;
  }

更新backward

下一个节点的backward指向x

1
2
3
4
5
6
7
x->backward = (update[0] == zsl->header) ? NULL : update[0];
if (x->level[0].forward)
    x->level[0].forward->backward = x;
else
    zsl->tail = x;
zsl->length++;
return x;

删除节点

删除节点，是插入的一个反向过程，同样的查找位置，删除节点，更新前一个节点和后一个节点的forward和backward，以及span

总结

跳跃表主要用于zset(有序集合)的实现

其查询、插入、删除的复杂度都是$O(\log{N})$

Tags: redis源码阅读 数据库
← hexo配置gitalk Redis基本数据结构-2 →

扫描二维码，分享此文章