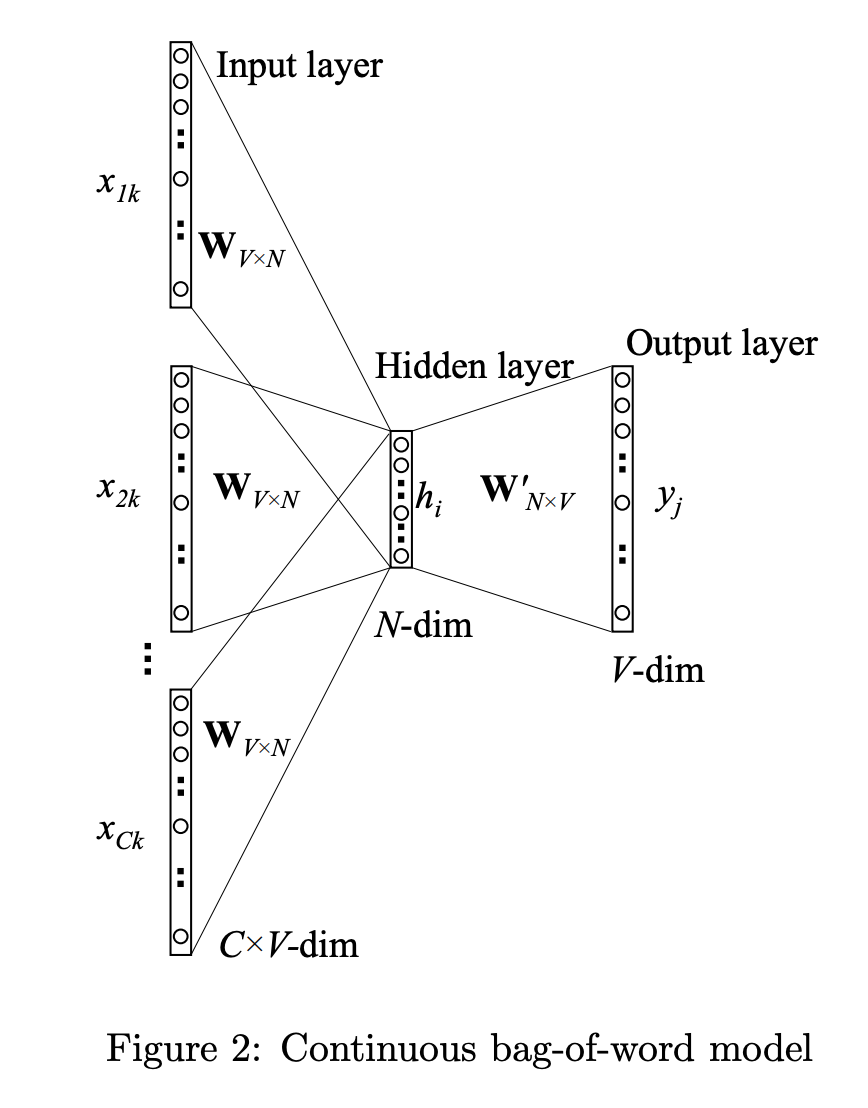
Continuous Bag-of-Word Model(CBOW)

One word

the vocabulary size is V , and the hidden layer size is N

CBOW: input is content words, output is target word

First, let’s see an simple model, one input word, one output word.

for example, two words [‘I’, ‘like’], input is ‘I’, output is ‘like’

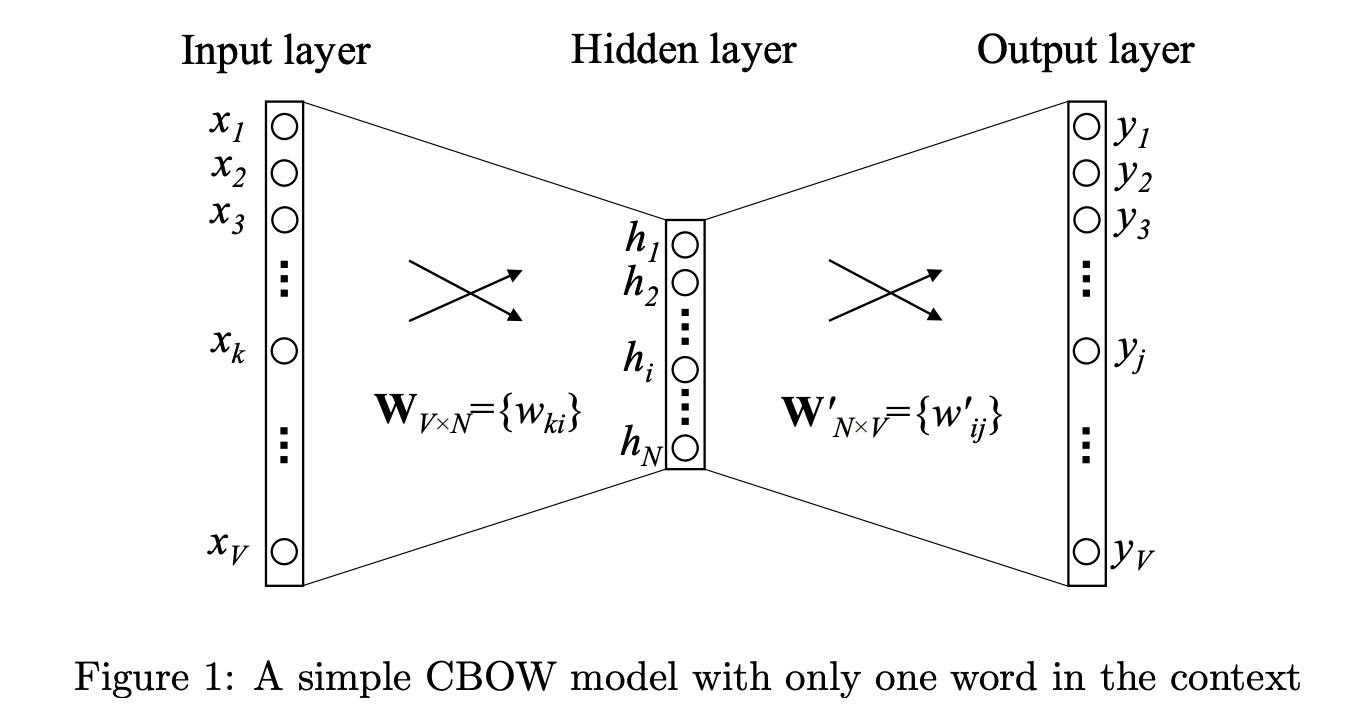
here, we use one-hot encode, ${x_1, x_2…x_v}$, form is $[0,1,…0]$(only one 1)

two weight matrix，$W$ and $W’$

Forward propagation

To get hidden layer：

$\mathbf{h} = \mathbf{W}^T \mathbf{x}$

$\mathbf h$ is $N * 1$ dimension

then we have a output vertor named $\mathbf W’$

$\mathbf u = \mathbf{W'}^T \mathbf h$

$\mathbf u$ is $V * 1$, same as $\mathbf x$

usually, we use softmax to get the probability.

$\mathbf y = softmax(\mathbf u)$

and it is vertor form, if we look at each element’s form of vector, we will get:

$\mathbf{h} = \mathbf{W}^T \mathbf{x} = \mathbf{W}_{(k,)}^T:= \mathbf v_{w_I}^T$

here, we know x is one-hot, so $xk = 1, x{k’}=0, k’ \neq k$, and it multiple with $W^T$,

for example:

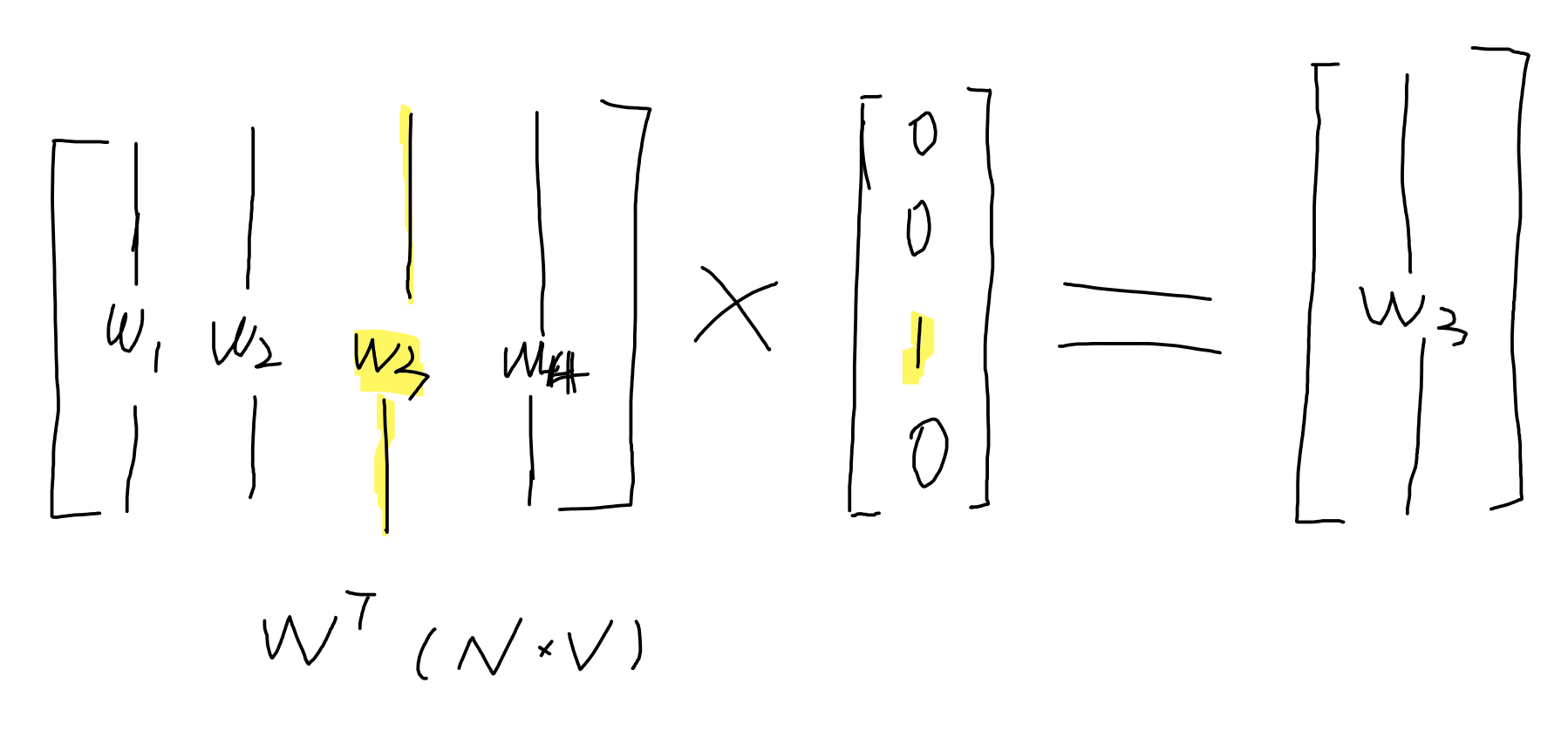
and for $\mathbf u$, each element of $\mathbf u$ should be:

$u_j = \mathbf {v'_{w_j}}^T\mathbf h$

for y:

$p(w_j|w_I) = y_j = softmax(u_j) =\frac{\exp \left(u_{j}\right)}{\sum_{j^{\prime}=1}^{V} \exp \left(u_{j^{\prime}}\right)}$

backward propagation

for hidden-output vector

according maximum likelihood estimation, we want

$\begin{aligned} \max p\left(w_{O} | w_{I}\right) &=\max y_{j^{*}} \\ &=\max \log y_{j^{*}} \\ &=u_{j^{*}}-\log \sum_{j^{\prime}=1}^{V} \exp \left(u_{j^{\prime}}\right) :=-E \end{aligned}$

y_true = [0, 1, 0, 0], y_pred = [0.1, 0.80, 0.01, 0.2], here $j^* = 1, y_{j^*}=0.8$, and we want $\max y_{j*}$

where $E=-\log p\left(w{O} | w{I}\right)$ is our loss function, and we want mininum it.

let’s get its derivative:

$\frac{\partial E}{\partial u_{j}}=y_{j}-t_{j} :=e_{j}$

here because loss is about $j^$, and derivative is about $j$, so we have $t_j = 1 \ when \ j = j^, else \ t_j = 0$

then go on:

$\frac{\partial E}{\partial w_{i j}^{\prime}}=\frac{\partial E}{\partial u_{j}} \cdot \frac{\partial u_{j}}{\partial w_{i j}^{\prime}}=e_{j} \cdot h_{i}$

that is good, we can use it in gradient descent

$w_{i j}^{'(new)}=w_{i j}^{'(old)}-\eta \cdot e_{j} \cdot h_{i}$

$\mathbf{v}_{w_{j}}^{'(new)}=\mathbf{v}_{w_{j}}^{'(old)}-\eta \cdot e_{j} \cdot \mathbf{h} \quad \text { for } j=1,2, \cdots, V$

for input-hidden vector

$\frac{\partial E}{\partial h_{i}}=\sum_{j=1}^{V} \frac{\partial E}{\partial u_{j}} \cdot \frac{\partial u_{j}}{\partial h_{i}}=\sum_{j=1}^{V} e_{j} \cdot w_{i j}^{\prime} :=\mathrm{EH}_{i}$ $h_{i}=\sum_{k=1}^{V} x_{k} \cdot w_{k i}$ $\frac{\partial E}{\partial w_{k i}}=\frac{\partial E}{\partial h_{i}} \cdot \frac{\partial h_{i}}{\partial w_{k i}}=\mathrm{EH}_{i} \cdot x_{k}$ $\frac{\partial E}{\partial \mathbf{W}}=\mathbf{x} \otimes \mathrm{EH}=\mathbf{x E H}^{T}$

for gradient descent

$\mathbf{v}_{w_{I}}^{(new)}=\mathbf{v}_{w_{I}}^{(old)}-\eta \cdot \mathbf E \cdot \mathbf{H}^T \quad$

Multi-word context

We use the average

$\begin{aligned} \mathbf{h} &=\frac{1}{C} \mathbf{W}^{T}\left(\mathbf{x}_{1}+\mathbf{x}_{2}+\cdots+\mathbf{x}_{C}\right) \\ &=\frac{1}{C}\left(\mathbf{v}_{w_{1}}+\mathbf{v}_{w_{2}}+\cdots+\mathbf{v}_{w_{C}}\right)^{T} \end{aligned}$

and

$\mathbf{v}_{w_{j}}^{\prime \ (new)}=\mathbf{v}_{w_{j}}^{\prime \ (old) }-\eta \cdot e_{j} \cdot \mathbf{h} \quad \text { for } j=1,2, \cdots, V$ $\mathbf{v}_{w_{I, c}}^{(new)}=\mathbf{v}_{w_{I,c}}^{(old)}-\frac{1}{C} \cdot\eta \cdot \mathbf E \cdot \mathbf{H}^T \quad$

Skip-Gram Model

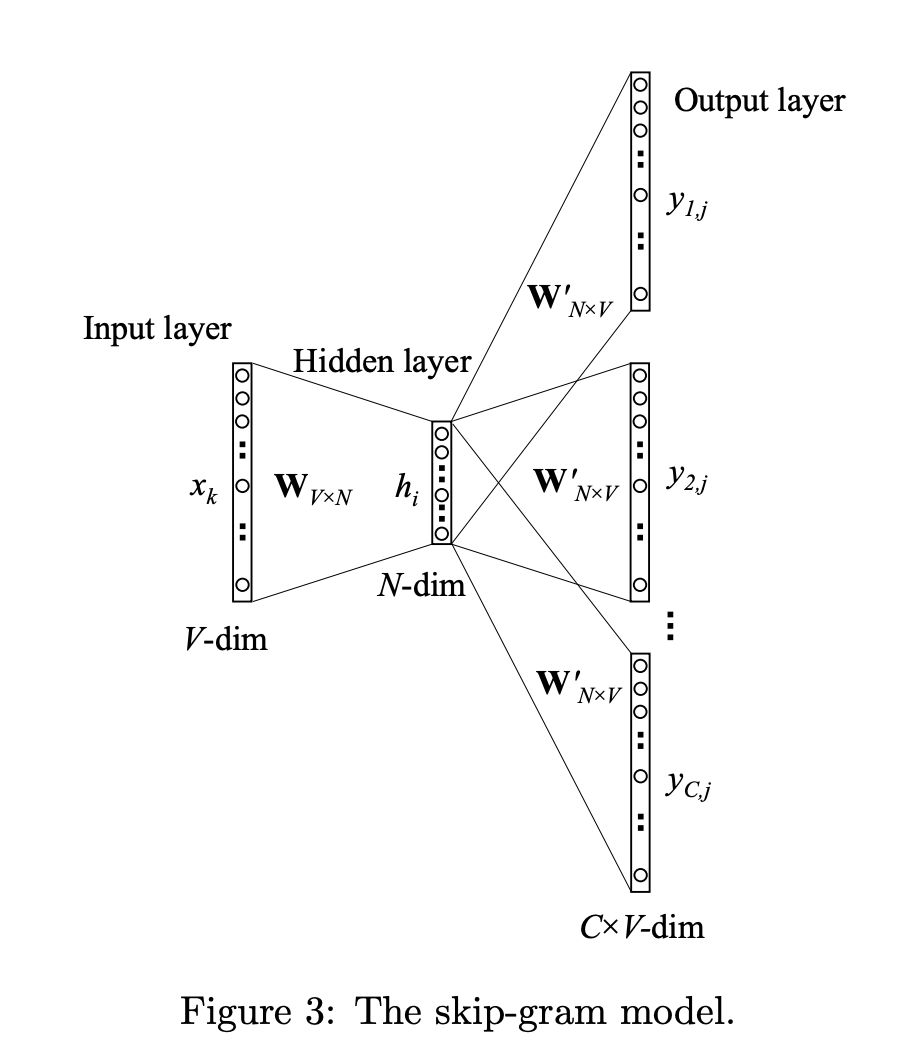
different with CBOW, skip-gram uses one word input and multiple output words.

for example, we have a word with one-hot $[0, 0, 1, 0, 0]$, and have 3 words which is assiociated,

so y will be $[1, 1, 0, 1,0]$

forward propagation

the calculation of input and hidden is same with CBOW.

$\mathbf{h}=\mathbf{W}_{(k, \cdot)}^{T} :=\mathbf{v}_{w_{I}}^{T}$

for hidden to output:

$p\left(w_{c, j}=w_{O, c} | w_{I}\right)=y_{c, j}=\frac{\exp \left(u_{c, j}\right)}{\sum_{j^{\prime}=1}^{V} \exp \left(u_{j^{\prime}}\right)}$ $u_{c, j}=u_{j}=\mathbf{v}_{w_{j}}^{\prime T} \cdot \mathbf{h}, \text { for } c=1,2, \cdots, C$

Note: in the Figure 3, we see there is C $W’{N*V}$, but actually they are one $W’{N*V}$,

and why so many y?

for example, like what we say before, the y is [1, 1, 0, 1, 0], for 3 words assiociated, and if we divide it to 3 vector, it is [1, 0, 0, 0, 0], [0, 1, 0, 0, 0], [0, 0, 0, 1, 0],

it explains why we have C output in Figure 3, but they have one shared weight.

backpropagation

For loss, it changed to

$\begin{aligned} E &=-\log p\left(w_{O, 1}, w_{O, 2}, \cdots, w_{O, C} | w_{I}\right) \\ &=-\log \prod_{c=1}^{C} \frac{\exp \left(u_{c, j_{c}^{*}}\right)}{\sum_{j^{\prime}=1}^{V} \exp \left(u_{j^{\prime}}\right)} \\ &=-\sum_{c=1}^{C} u_{j_{c}^{*}}+C \cdot \log \sum_{j^{\prime}=1}^{V} \exp \left(u_{j^{\prime}}\right) \end{aligned}$

For hidden-output vector

and derivative, each word in C

$\frac{\partial E}{\partial u_{c, j}}=y_{c, j}-t_{c, j} :=e_{c, j}$

so, sum it:

$\mathrm{EI}_{j}=\sum_{c=1}^{C} e_{c, j}$ $\frac{\partial E}{\partial w_{i j}^{\prime}}=\sum_{c=1}^{C} \frac{\partial E}{\partial u_{c, j}} \cdot \frac{\partial u_{c, j}}{\partial w_{i j}^{\prime}}=\mathrm{EI}_{j} \cdot h_{i}$

gradient descent

$w_{i j}^{'(new)}=w_{i j}^{'(old)}-\eta \cdot EI_{j} \cdot h_{i}$

$\mathbf{v}_{w_{j}}^{'(new)}=\mathbf{v}_{w_{j}}^{'(old)}-\eta \cdot E_{j} \cdot \mathbf{h} \quad \text { for } j=1,2, \cdots, V$

For input-hidden vector

$\mathbf{v}_{w_{I}}^{(new)}=\mathbf{v}_{w_{I}}^{(old)}-\eta \cdot \mathbf E \cdot \mathbf{H}^T \quad$

where $\mathbf{EH}$ is an N-dimension vector, each component of which is defined as:

$\mathrm{EH}_{i}=\sum_{j=1}^{V} \mathrm{EI}_{j} \cdot w_{i j}^{\prime}$

← FreeRTOS-schedule Nginx安装和使用 →

扫描二维码，分享此文章

word2vec_paper_reading