XGBoost

XGBoost本身属于随机森林的范畴，在详细点的话，属于Gradient Tree Boosting的范畴，首先，随机森林是很容易过拟合，XGBoost在Gradient Tree Boosting之上，在计算Loss的时候，引入了回归，通过回归解决过拟合的问题。

那么，来看一看XGBoost的论文，看下它到底是怎么回事。

Regularized Learning Objective

首先，对于数据集$\mathcal{D}=\left{\left(\mathbf{x}{i}, y{i}\right)\right}\left(|\mathcal{D}|=n, \mathbf{x}{i} \in \mathbb{R}^{m}, y{i} \in \mathbb{R}\right)$，如果一个树模型，采用了K个函数，来拟合输出，

那么

$\hat{y}_{i}=\phi\left(\mathbf{x}_{i}\right)=\sum_{k=1}^{K} f_{k}\left(\mathbf{x}_{i}\right), \quad f_{k} \in \mathcal{F} \tag{1}$

对此，我们可以得到Loss

$\begin{array}{l}{\mathcal{L}(\phi)=\sum_{i} l\left(\hat{y}_{i}, y_{i}\right)+\sum_{k} \tag{2} \Omega\left(f_{k}\right)} \\ {\text { where } \Omega(f)=\gamma T+\frac{1}{2} \lambda\|w\|^{2}}\end{array}$

对于 $(x_i, y_i)$，我们得到$x_i, \hat{y}_i$之后，可以计算相应的Loss，$\omega$在这里是不同子叶的权重

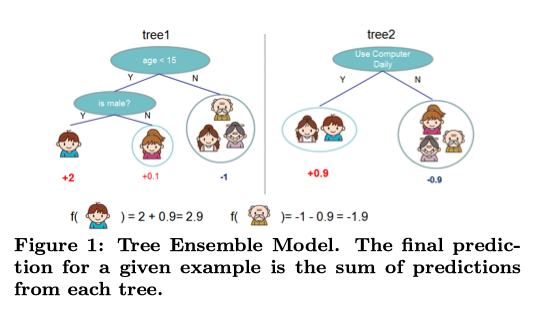
这幅图可以帮助理解上述公式

Gradient Tree Boosting

那么，Gradient Tree Boosting是怎么一回事呢

Gradient Tree Boosting通过建立多个树，把上一个树的偏差，当做下一个树的学习目标

比如，$y=1$，经过第一个树之后，$\hat{y_1}=0.7$，那么，下一轮的$y=0.3$，并使用新的$f(x)$去获取这个目标

由此，可以将式2，拓展为：

$\mathcal{L}^{(t)}=\sum_{i=1}^{n} l\left(y_{i}, \hat{y}_{i}^{(t-1)}+f_{t}\left(\mathbf{x}_{i}\right)\right)+\Omega\left(f_{t}\right) \tag{3}$

这里，$\hat{y_i}^{t-1}$即第$t-1$个树的输出

将上式泰勒展开

$\mathcal{L}^{(t)} \simeq \sum_{i=1}^{n}\left[l\left(y_{i}, \hat{y}^{(t-1)}\right)+g_{i} f_{t}\left(\mathbf{x}_{i}\right)+\frac{1}{2} h_{i} f_{t}^{2}\left(\mathbf{x}_{i}\right)\right]+\Omega\left(f_{t}\right) \tag{4}$

这里$g{i}=\partial{\hat{y}^{(t-1)}} l\left(y{i}, \hat{y}^{(t-1)}\right) \text { and } h{i}=\partial{\hat{y}^{(t-1)}}^{2} l\left(y{i}, \hat{y}^{(t-1)}\right)$

分别是一阶导数和二阶导数

然后，对于第$t$次迭代来说，$l\left(y_{i}, \hat{y}^{(t-1)}\right)$是已知的常量，式4可以被简化

$\tilde{\mathcal{L}}^{(t)}=\sum_{i=1}^{n}\left[g_{i} f_{t}\left(\mathbf{x}_{i}\right)+\frac{1}{2} h_{i} f_{t}^{2}\left(\mathbf{x}_{i}\right)\right]+\Omega\left(f_{t}\right) \tag{5}$

定义$I{j}=\left{i | q\left(\mathbf{x}{i}\right)=j\right}$, 参考下图，$I_j$是属于第$j$个叶子的$x$的index

做这样一个转换的目的，是为了将对$i$的求和，转化为对$j$的求和，同时展开$\Omega(f_t)$，一起计算

$\begin{aligned} \tilde{\mathcal{L}}^{(t)} &=\sum_{i=1}^{n}\left[g_{i} f_{t}\left(\mathbf{x}_{i}\right)+\frac{1}{2} h_{i} f_{t}^{2}\left(\mathbf{x}_{i}\right)\right]+\gamma T+\frac{1}{2} \lambda \sum_{j=1}^{T} w_{j}^{2} \\ &=\sum_{j=1}^{T}\left[\left(\sum_{i \in I_{j}} g_{i}\right) w_{j}+\frac{1}{2}\left(\sum_{i \in I_{j}} h_{i}+\lambda\right) w_{j}^{2}\right]+\gamma T \end{aligned} \tag{6}$

目的，是让Loss最小(为0)，即得到此时的

$w_{j}^{*}=-\frac{\sum_{i \in I_{j}} g_{i}}{\sum_{i \in I_{j}} h_{i}+\lambda} \tag{7}$

把式7带入式6

$\tilde{\mathcal{L}}^{(t)}(q)=-\frac{1}{2} \sum_{j=1}^{T} \frac{\left(\sum_{i \in I_{j}} g_{i}\right)^{2}}{\sum_{i \in I_{j}} h_{i}+\lambda}+\gamma T \tag{8}$

这就得到了最终的Loss函数

此外还有一个问题是，什么时候建立新树？

论文里，提出，通过计算左右子树的Loss和树的差值，来判断是否建立新树

$\mathcal{L}_{s p l i t}=\frac{1}{2}\left[\frac{\left(\sum_{i \in I_{L}} g_{i}\right)^{2}}{\sum_{i \in I_{L}} h_{i}+\lambda}+\frac{\left(\sum_{i \in I_{R}} g_{i}\right)^{2}}{\sum_{i \in I_{R}} h_{i}+\lambda}-\frac{\left(\sum_{i \in I} g_{i}\right)^{2}}{\sum_{i \in I} h_{i}+\lambda}\right]-\gamma \tag{9}$

这个式子，表示，$\mathcal{L}_{s p l i t}$越大，说明左右子树的Loss越大，应该把左右子树”劈开”，产生新树

以上，就是XGBoost的算法推导。

Ref

XGBoost: A Scalable Tree Boosting System

Tags: Machine Learning

← Naive Bayes Classifier BLE-MESH-Architecture →

扫描二维码，分享此文章