Naive Bayes Classifier

什么是贝叶斯

贝叶斯是一种概率定理，

$p(c|X) = \frac{p(c, X)}{p(X)} = \frac{p(X|c)p(c)}{p(X)}\tag{1}$

如果$X$是由一系列特征$x_1, x_2, x_3…x_n$组成

根据全概率定理，可以将$p(c,x)$展开

$p(c, X) = p(c, x_1, x_2, x_3 … x_n) = p(x_1|x_2,x_3…x_n,c)p(x_2|x_3…x_n,c)p(x3|…x_n,c)…p(x_n|c)p(c)$

即

$p(c|X) = \frac{p(x_1|x_2,x_3…x_n,c)*p(x_2|x_3…x_n,c)*p(x3|…x_n,c)…p(x_n|c)*p(c)}{p(X)}\tag{2}$

什么是朴素贝叶斯

朴素贝叶斯是指一种简化手段，对于多种条件下的概率，认为各个条件是互相独立的，

所以对于，$p(x_1|x_2,x_3…x_n,c) \approx p(x_1|c)$

式2，即简化为：

$p(c|X) \approx \frac{p(x_1|c)*p(x_2|c)*p(x3|c)…p(x_n|c)*p(c)}{p(X)} = \frac{p(c)\prod_{i=1}^np(x_i|c)}{p(X)}\tag{3}$

该式可以进一步简化为

$p\left(y | x_{1}, \ldots, x_{n}\right) \propto p(y) \prod_{i=1}^{n} p\left(x_{i} | y\right)\tag{4}$

对于$p(x_1|c)$这类概率，如果$X$是离散的，那么可以直接根据古典概型，求出对应概率。

如果$X$是连续变量，一般会设定一个假设，假设$X$的分布，满足高斯分布/多项式分布/伯克利分布等分布，并根据这些分布，求出对应的概率。

这里，主要讨论比较常见的高斯分布(正太分布)

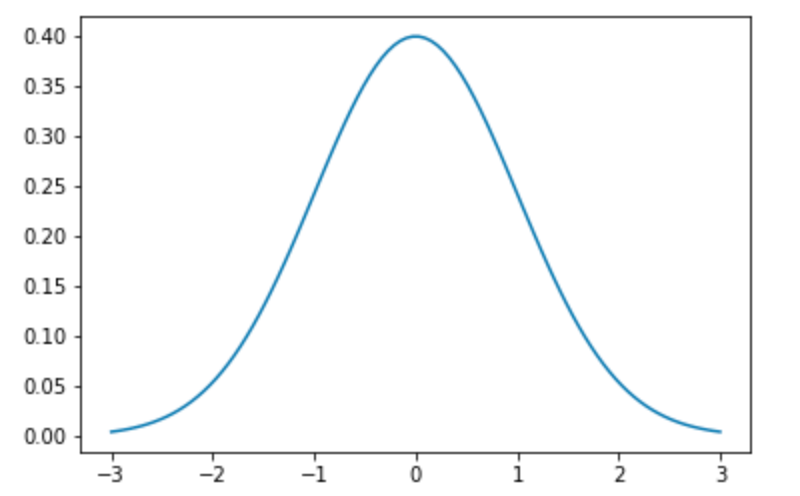
高斯分布

高斯分布的概率密度函数

$f_{X}(x)=\frac{1}{\sqrt{2 \pi \sigma^2} } \mathrm{e}^{-(x-\mu)^{2} /\left(2 \sigma^{2}\right)}\tag{5}$

这里$\mu和\sigma$分别是平均值和标准差

$\mu = 0, \sigma = 1$

即$X$满足高斯分布

$P\left(x_{i} | y\right)=\frac{1}{\sqrt{2 \pi \sigma_{y}^{2}}} \exp \left(-\frac{\left(x_{i}-\mu_{y}\right)^{2}}{2 \sigma_{y}^{2}}\right)\tag{6}$

最大似然估计

在分类问题中，$y$通常会有多个类别，那么，在已知$X$的前提下，应该选择哪个$y$作为输出呢？

这里，基于最大似然估计原理，根据$X$，求出每一个$y$的概率，其中概率最大的$y$，作为输出

则式4可以转化为:

$\hat{y}=\arg \max _{y} p(y) \prod_{i=1}^{n} p\left(x_{i} | y\right)$

通常，出于计算简便考虑，对式4做对数处理，

$\ln p\left(y | x_{1}, \ldots, x_{n}\right) \propto \ln \big(p(y) \prod_{i=1}^{n} p\left(x_{i} | y\right) \big) = \ln p(y) + \sum_{i=1}^n\ln p(x_i|y)$ $\hat{y}=\arg \max _{y} \big( \ln p(y) + \sum_{i=1}^n\ln p(x_i|y) \big) \tag{7}$

根据式7，已经可以手撸一个贝叶斯分类器了。

关于，为什么要取对数的原因，由于$p \in [0, 1]$, 连续乘积往往会结果非常小，甚至超出计算机精度，导致归0，所有用对数

Coding

一个基于Python的朴素贝叶斯实现

class BayesCluster:
    def __init__(self, train_x, train_y):
        self.train_x = train_x
        self.train_y = train_y
        
        self.prepare()
        
    def prepare(self):
        self.classifier = list(set(self.train_y))
        
        self.mean = [np.mean(self.train_x[self.train_y==cls, :], axis=0) for cls in self.classifier]
        self.std = [np.std(self.train_x[self.train_y==cls, :], axis=0) for cls in self.classifier]
        self.mean = np.array(self.mean)
        self.std = np.array(self.std)
    
        self.p_classifier = [len(self.train_x[self.train_y==cls]) / len(self.train_x) for cls in self.classifier]
        
    def likehood(self, x, cls_idx):
        mean = self.mean[cls_idx,:]
        std = self.std[cls_idx,:]
        p_cls = self.p_classifier[cls_idx]
        
        joint = -np.sum(np.log(np.sqrt(2 * np.pi) * std)) - \
                    np.sum(np.power(x - mean, 2) / (2 * np.power(std, 2)))

        return joint + np.log(p_cls)
    
    def predict(self, test):
        y_hat = []
        
        for vector in test: 
            p_y = [self.likehood(vector, i) for i in range(len(self.classifier))]
        
            y_hat.append(self.classifier[np.argmax(p_y)])
                
        return np.array(y_hat)

在二分类问题上，简单测试，precision和recall同GaussianNB表现一致

参考

scikit-learn naive bayes

Scikit-learn GaussianNB source code

概率导论3.3正太随机变量

概率导论9.1.2 最大似然估计

Tags: Machine Learning

← Hexo的多语言配置 XGBoost →

扫描二维码，分享此文章